誘導制御

航法誘導制御とは

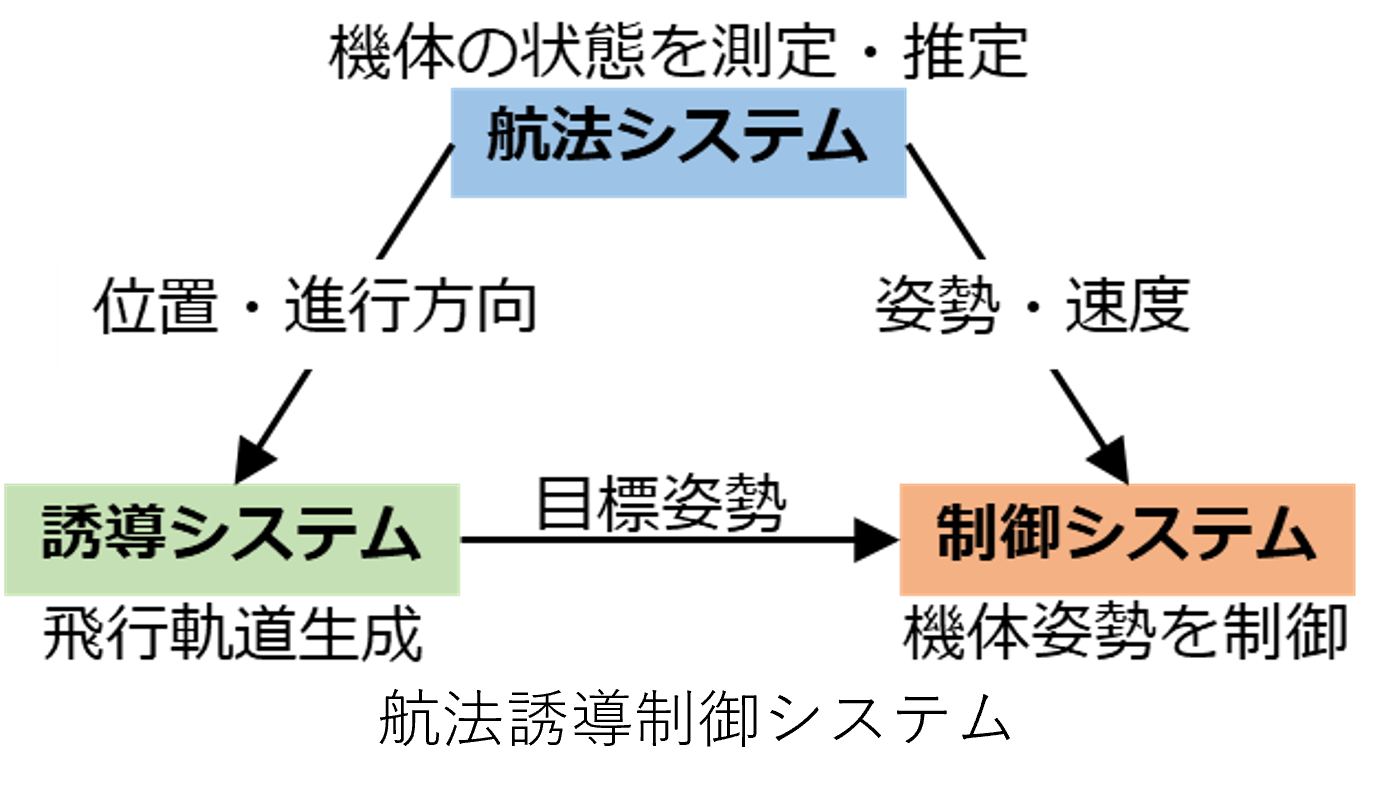
航法誘導制御技術は，ロケットや航空機など自律航行するシステムにとって重要な要素です．航法システムから得られた機体の状態量をもとに，誘導システムが飛行可能な目標軌道を生成し，それを実現するための目標状態量を制御システムへ与えます．制御システムは目標状態量に追従するように制御デバイスを操作することで目標軌道を実現させます．

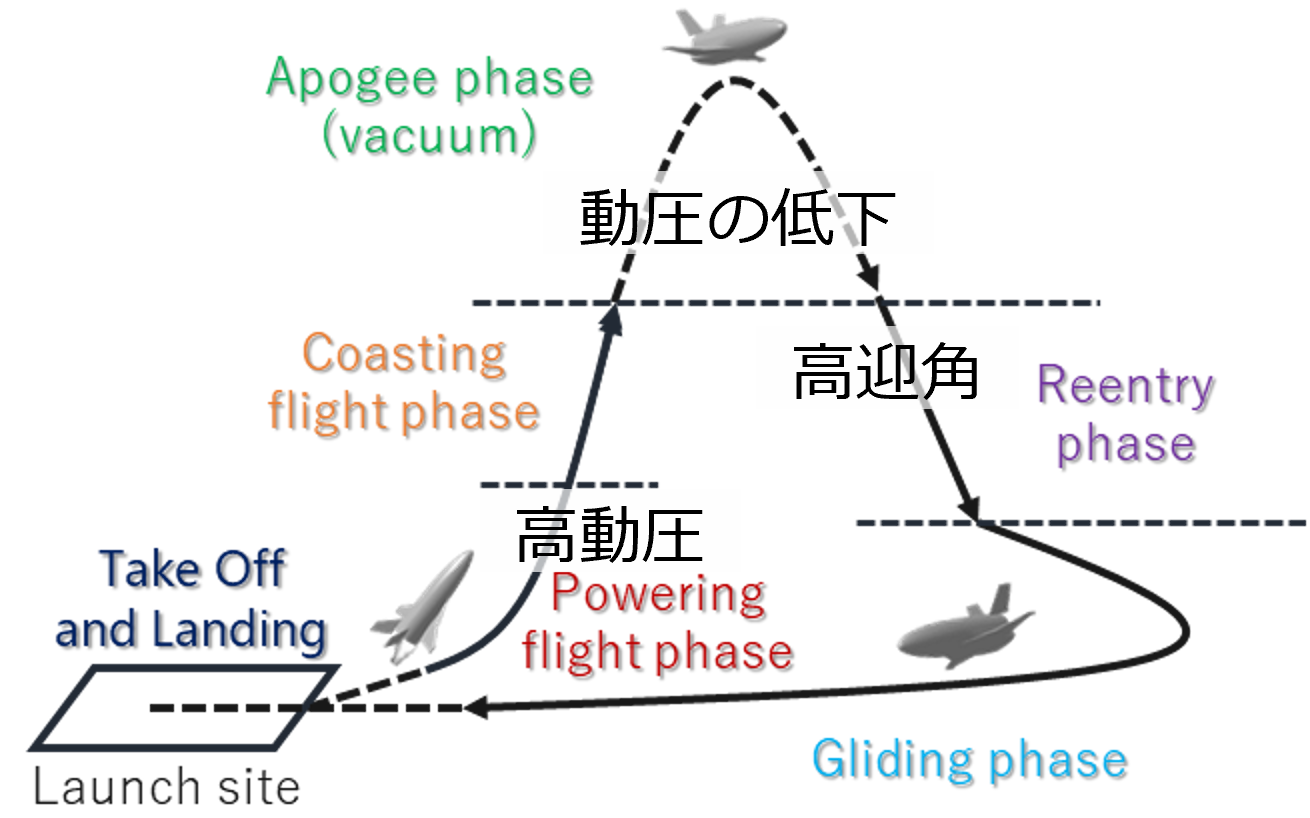
一般的な航空機や使い捨てロケットとは異なり，スペースプレーンは推力上昇，再突入，滑空飛行など動圧や姿勢変化の幅広い飛行領域を有します．そのため，事前に設計した軌道や古典制御を用いた飛行は困難です．本研究室では，想定していない軌道や外乱に対応できる自律型の誘導則と制御則を研究するとともに実験機を用いた実証を行っています．

 

誘導

誘導では不確かさがある状況でも計画された目標地点へ到達することが求められます．また，非常時においても迅速にミッションを中断し帰還することも重要です．本研究ではこの誘導の実現に向けて，リアルタイムにおける軌道生成を行うための1 ) 軌道生成に関する研究と 2 )生成された軌道の良し悪しを判断する最適化の研究を行っています．

■ 軌道生成

スペースプレーンは飛行軌道の成立性が厳しいため，軌道の最適化に関しては単に最適化計算を適用しただけでは計算時間が増大し計算資源の限られた機上の計算機での実行が困難となります．そのため軌道生成では飛行状態に着目し，軌道の順設計・逆設計問題を組み合わせた研究を進めています．

  • 軌道の順設計問題

上昇から再突入にかけての飛行では，機械・構造的な制約を満たしつつ複雑に変化する縦のトリム制約へ対応することが重要です．軌道の順設計問題においてはフーリエ級数で直接制御入力を設計し，状態方程式を積分することで軌道を生成しています．また，上昇時には経路角が90度付近でも特異点に陥ることがない，クォータニオンを適用した状態方程式を用いることで，自由度の高い軌道を生成する研究も進めています．

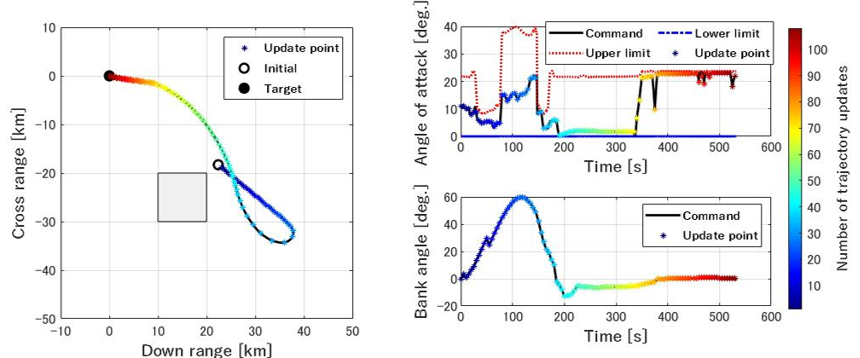
  • 軌道の逆設計問題

滑走路へ帰還する際には無推力による滑空飛行で所望の終端位置，進入角度，速度というような強い制約が課せられます．軌道の逆設計では先に複数のベジェ曲線を接続したスプラインによる経路形状の設計を行い，軌道の逆ダイナミクスを解くことで誤差なく滑走路へ帰還する誘導コマンドを得る手法を取り入れています．また，滑走路へ所望の進入条件を満たすために機体が保有する力学的エネルギを制御する研究にも取り組んでいます．

 

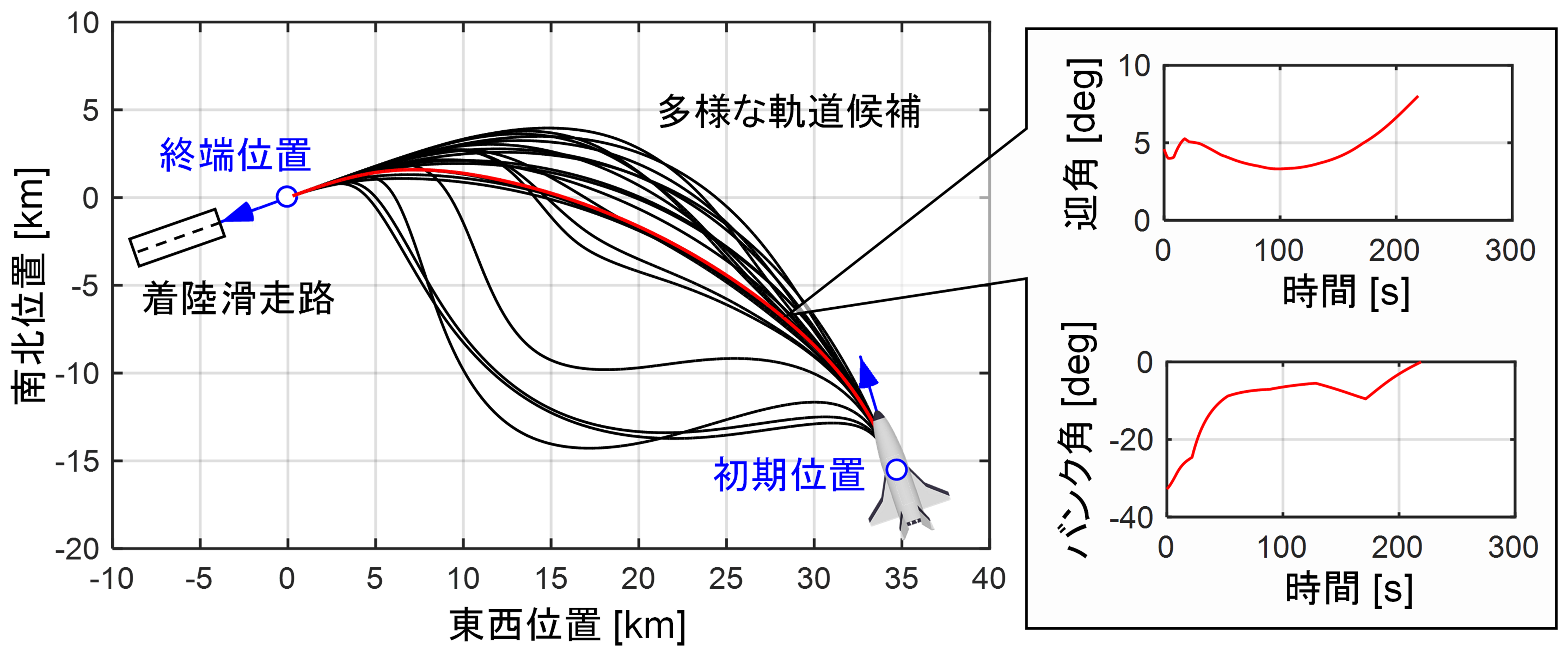
■ 最適化

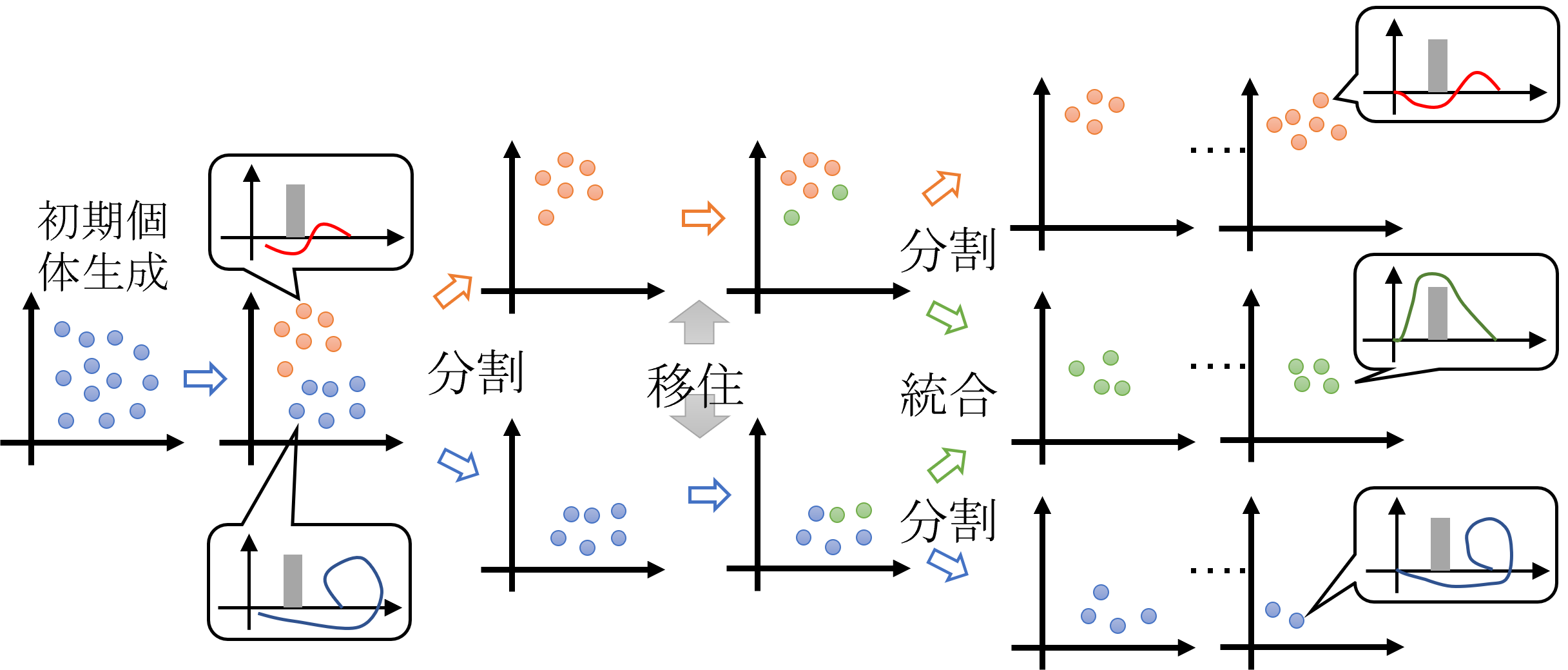
本研究では動的分散遺伝的アルゴリズム（DynDGA）という進化計算手法を開発し，大域的な最適解を探索します．軌道の地上航跡を特徴量として数世代毎に母集団をクラスタリングし，個々のクラスタで独立した進化を行うことで多様性を維持しつつ特徴的な複数の解軌道の選択が可能となっています．この最適化により飛行開始から終了までの全飛行を通して最適な軌道を生成する手法の研究を進めています．

 

制御

■ ダイナミックインバージョン理論を用いた姿勢制御

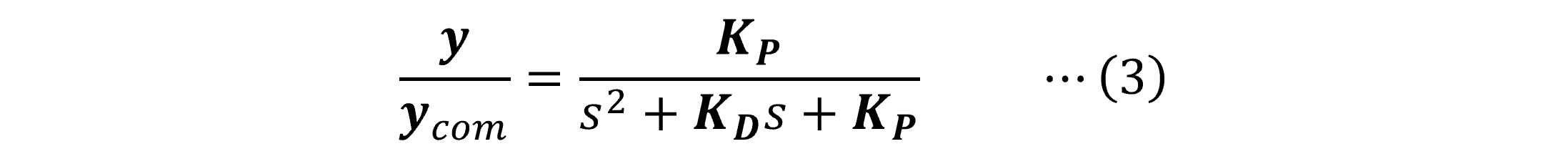本研究室では，誘導則から得られる目標姿勢に追従するため，ダイナミックインバージョン（DI：Dynamic Inversion）理論を用いた姿勢制御手法について研究しています． DI理論は，制御量と制御入力の関係に着目することで非線形システムに対しても線形な応答を与えられる制御手法です．この際，設計者が任意に設定可能な入力（疑似入力 ν）を導入することで，閉ループ系に任意の線形応答を与えることが可能となります．本研究室で扱う有翼ロケットの姿勢制御では，制御量と制御入力の関係は式（１）となり，制御入力のコマンドは式（２）のように算出できます．例として疑似入力にPD制御を採用した場合，閉ループ系は式（３）のように二次の線形応答で表現できます．　また本研究室では，推力飛行及び無推力飛行におけるDI理論を用いた制御系設計の他，応答速度の違いによりシステムを階層化してDI理論を適用する多階層DI理論を用いたスペースプレーンへの適用に関する研究も行っています．

 

■ 飛行環境適応型ゲイン調整法

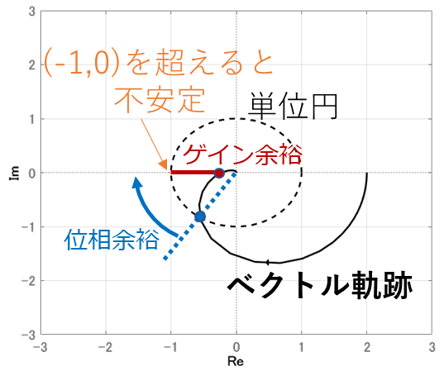
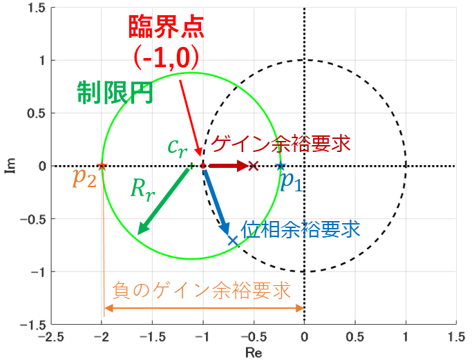
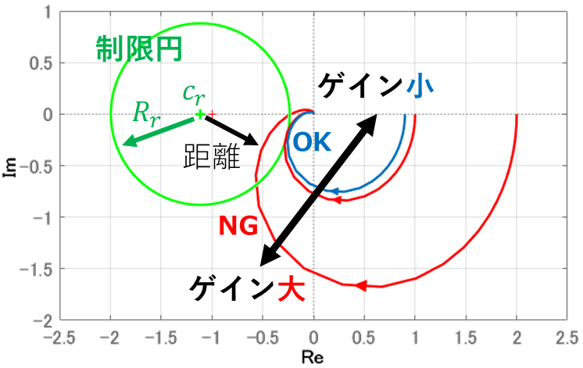
制御システムを構築する際，外乱に対する安定性を保証する必要があります．線形制御ではロバスト性を評価する指標として安定余裕が用いられています．本研究室では，DI理論を用いた制御則に対して飛行中に自動で安定余裕を保証する手法を研究しています．複素平面上における安定余裕の定義とベクトル軌跡の関係に着目すると，安定余裕を満たさない領域を円で定義できます（制限円）．ベクトル軌跡と制限円の内外判定を行うことで任意の安定余裕をもつ制御ゲインに調整します．制御周期ごとに調整し，想定されていない軌道や外乱においてもロバスト性を有する制御を可能とします．理論や探索手法に加え，実際に搭載するマイコンを用いて計算コストを評価することで実用化を目指しています．

ベクトル軌跡と安定余裕

制限円の定義

ベクトル軌跡と制限円

 

■ クォータニオン表現を用いた有翼ロケットの姿勢制御

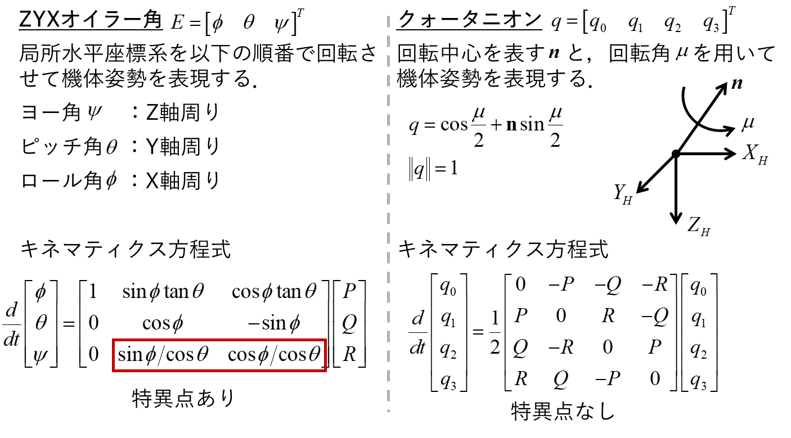
有翼ロケットは，一般的な航空機と異なり垂直離陸をします．そのため， ZYXオイラー角で姿勢表現をするとピッチ角が90度となり，ロール角とヨー角が連成してしまい機体姿勢を正確に表現できなくなります．この課題を解決するため，本研究室では特異点を持たないクォータニオンを使用したDI制御則を提案しました．また目標姿勢と現在の姿勢との差を表す偏差クォータニオンに着目することで，特異点にとらわれずに任意の目標値を与えて制御することが可能となります．現在は，クォータニオンを用いた姿勢制御則に対する安定余裕保証法の研究を進めています．

 

■ 最小エネルギー制御による制御デバイスの駆動量最適化

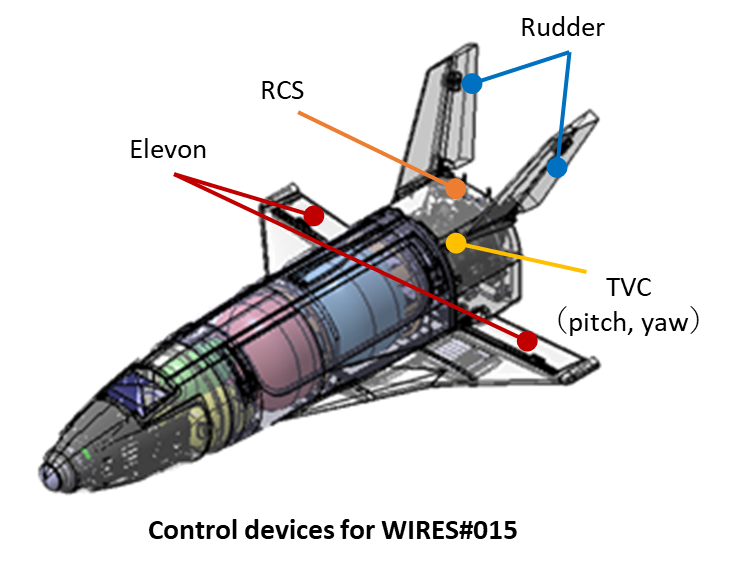
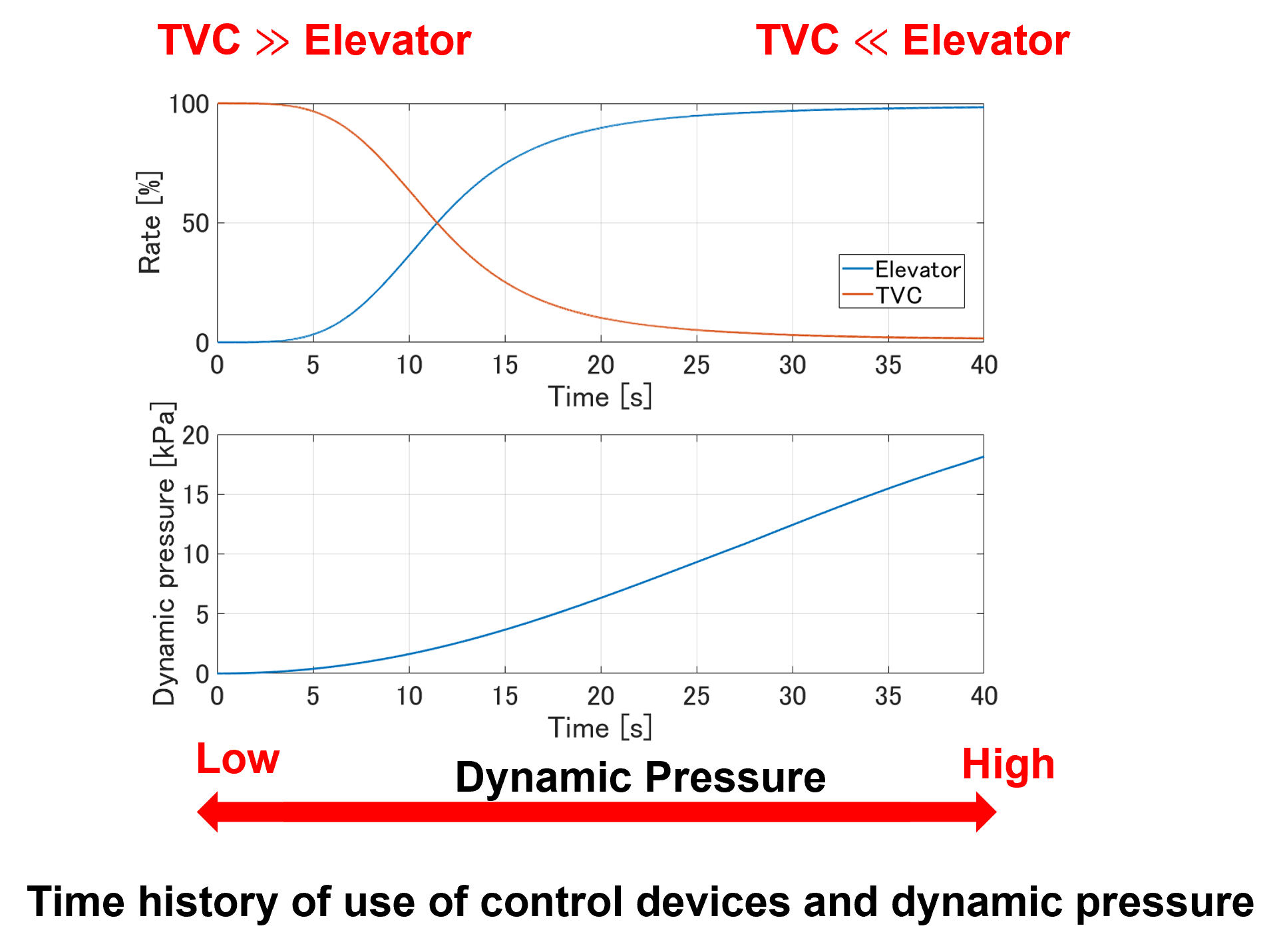
現在開発中の有翼ロケットでは，リフトオフ直後からエンジンカットオフまでの推力飛行中には動翼（エルロン，エレベーター，ラダー）と，エンジンの推力の向きを変更することで姿勢の制御を可能とするTVC（Thrust Vector Control）を併用して姿勢制御を行います．そのため，制御量として姿勢角（３つ）を，制御入力として制御デバイス（５つ）を採用すると制御入力が冗長となり，制御デバイスの駆動量が一意に決まらないという課題が発生します．この課題を解決するため，本研究室では最小エネルギー制御を用いた舵角割り当ての最適化を提案しています．最小エネルギー制御は制御デバイスの駆動量を最小にした効率の良い制御を目的としており，これにより低動圧時にはTVCを，動圧が上がってからは動翼を優先して使用した制御が可能となります．

 

 

«

»